
旧暦のいろいろ その1
最後に、旧暦にかかわるいろいろな情報をまとめていきましょう。
まず、はっきりさせないといけないのは、公式な旧暦、というものは存在しません。社会生活の基本となる暦が、いくつもあっては困ります。昔は使われていたものの、今では公式ではないので 「旧暦」と呼ばれるわけです。
ですから、乱暴に言えば、「これが私の旧暦」として、独自研究の旧暦を発表してもかまわないわけです。「どの旧暦が正しいか」という議論は無意味です。
そうは言っても「なんでもあり」では困るので、一般的な旧暦を紹介しましょう。一般に使われている旧暦は、明治の改暦まで使われていた「天保暦」という暦の計算方法を使って求めるもの、のようです。天保年間最後の年、1844年から、1872年まで施行されたものです。
天保とか言うと、はるか昔のようなイメージですが、西暦に直すと1830年から1844年、江戸時代には違いありませんが、明治元年が1868年ですから、そんなに昔ではないんですよね。
時代劇で有名な遠山の金さんもこの時代の人なんだそうです。ちょっと親近感(笑) ということで、桜の写真でもどうぞ。

図1 富士と桜
月の解説で何度も出てきましたが、「旧暦」は、太陰太陽暦です。月の満ち欠けを1ヶ月として、季節の移り変わりを太陽の動きで定めるものです。天保暦は、西洋の天文学知識を組み込んで作られ、太陰太陽暦の中でもかなり優れたものだったそうです。
二十四節気
太陰太陽暦は、季節の移り変わりについては太陽を基準としています。その基準こそが「二十四節気」。いまでは、ニュースや天気予報の話題程度にしか使われませんが、旧暦を使っていた時代には、二十四節気を基準に季節を決定していましたから、非常に重要な役割を担っていたわけです。
| 名前 | 現在の暦 | 種類 | 定義 (太陽黄径) |
名前 | 現在の暦 | 種類 | 定義 (太陽黄径) |
|---|---|---|---|---|---|---|---|
| 立春 | 2月 6日頃 | 正月節 | 315度 | 立秋 | 8月 6日頃 | 七月節 | 135度 |
| 雨水 | 2月21日頃 | 正月中 | 330度 | 処暑 | 8月21日頃 | 七月中 | 150度 |
| 啓蟄 | 3月 6日頃 | 二月節 | 345度 | 白露 | 9月 6日頃 | 八月節 | 165度 |
| 春分 | 3月21日頃 | 二月中 | 0度 | 秋分 | 9月21日頃 | 八月中 | 180度 |
| 清明 | 4月 6日頃 | 三月節 | 15度 | 寒露 | 10月 6日頃 | 九月節 | 195度 |
| 穀雨 | 4月21日頃 | 三月中 | 30度 | 霜降 | 10月21日頃 | 九月中 | 210度 |
| 立夏 | 5月 6日頃 | 四月節 | 45度 | 立冬 | 11月 6日頃 | 十月節 | 225度 |
| 小満 | 5月21日頃 | 四月中 | 60度 | 小雪 | 11月21日頃 | 十月中 | 240度 |
| 芒種 | 6月 6日頃 | 五月節 | 75度 | 大雪 | 12月 6日頃 | 十一月節 | 255度 |
| 夏至 | 6月21日頃 | 五月中 | 90度 | 冬至 | 12月21日頃 | 十一月中 | 270度 |
| 小暑 | 7月 6日頃 | 六月節 | 105度 | 小寒 | 1月 6日頃 | 十二月節 | 285度 |
| 大暑 | 7月21日頃 | 六月中 | 120度 | 大寒 | 1月21日頃 | 十二月中 | 300度 |
上の表の中に「種類」という欄があり、そこに「正月節」とか、「二月中」とかあります。これが、季節の移り変わりを表すものです。
「中」と「節」の2種類がありますが、「節」が季節の、「中」が月の基準とされています。たとえば、「立春」は「正月節」ですから、この日以降を春とする、「春分」は「二月中」とありますから、「春分」を含んだ1ヶ月間を「二月」とするわけです。
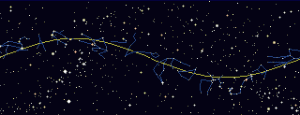
図2 黄道(上)と黄道座標系(下)
星図作成: StellaNavigator
天保暦で使われた、そして現在も使われている二十四節気の定義では、「立春」や「春分」を決めるのは、太陽の実際の位置です。その座標が、上の「定義」にもまとめてあります。
太陽黄径というのは、黄道座標系での経度のこと、黄道座標系は、1年かけて太陽が動いていくその経路を基準にした座標系のことです(図2)
たとえば、現在の暦で10月下旬にある「降霜」は、太陽が黄径210度の位置に来た瞬間、と定義されています。現在の二十四節気は実際の太陽の位置によって決められている訳です。
そんなこと、太陽の位置を基準にして季節を決めているんだから当たり前だ、と思いますが、実はこれ、大変なことです。
地球は、とても円に近いとはいえ楕円を描いて太陽を周っていますから、季節によって、太陽の年周運動も早くなったり遅くなったりします。つまり、二十四節気のそれぞれの経過時間は一定ではないのです。
太陽の年周運動速度が一定でないこと、そのことを観測し、理解し、将来に渡って計算できるようになって始めて、そのことを暦に組み込めるわけです。
西洋の天文学知識を組み込んで作られ、太陰太陽暦の中でもかなり優れたものだった、というのは、まさにこれのことでしょう。それに対し、天保暦よりも昔の暦は、冬至の日を基準として1年を均等に24で割って、太陽の年周運動速度が一定として求めていました。
二十四節気というと、昔の暦、旧暦に関係するもの、という印象ですが、実は、今でも立派に使える季節の目印だったんですね。
旧暦(天保暦)
では、旧暦(天保暦)の定義をまとめてみましょう。
- 太陽と月の黄径が一致する時を朔とする(=現在の新月の定義と同じです)
- 朔を含む日を一日とし、次の朔までを一ヶ月とする
- 太陽の通り道、黄道を、冬至を基準に12等分し、それを中気とする。
- 冬至を含む月を十一月、春分を含む月を二月、夏至は五月、秋分は八月、とする。
- 中気を含まない月を閏月とすることがある
1.と2.が1ヶ月の定義、3.と4.が季節の定義となっています
朔、というのは、月の解説でも書きましたが、新月のこと。「中気」は上で書いた「中」のことです。二十四節気は「中」と「節」が半分ずつですから、「中」は、黄道を12等分していますね。
3.と4.により、二、五、八、十一月が決められ、各季節の三ヶ月は、その一ヶ月ごとに「中」が入っていれば、二十四節気表の「種類」の「何月中」で、「何月」かが決定されるわけです。
現在の暦の感覚だと、二、五、八、十一月が決まれば、各季節の三ヶ月は自動的に、たとえば二月の次は三月、前が正月と自動的に決まるように思いますが、わざわざくどく書いたのは、旧暦の場合、「閏月」が入る可能性があるためです。
閏月
現在の暦、太陽暦では、1年は365日、うるう年は366日なのはご存知の通り。地球が太陽の周りを一回転するのに要する時間は365.24日、その端数を4年に一度、1日として清算しているわけです。
太陽暦の一ヶ月は30日か31日、2月だけ28日か29日になっています。

図3 「一ヶ月」と「新月」と「中」の関係
この場合、一ヶ月に「中」が2回あります。
太陰太陽暦では、一ヶ月は月の満ち欠けで決まります。月の満ち欠けの時間は約29.53日。一ヶ月は29日か30日となりますね。1年を12ヶ月とすると354日、太陽で測った1年の365日には11日足りません。そこで、厳密には19年に7回、約3年に一度、「閏月」を入れます。
旧暦の定義の5.は、まさに閏月を入れる基準を示したものです。
上で書いたとおり、地球の公転軌道が楕円のせいで、「中」から次の「中」までの経過時間は一定ではありません。29.4日から31.5日くらいとなります。
似たような数字がいっぱい出てきて混乱しそうですが、新月から新月までの時間が29.53日ですから、新月の前後に「中」を迎えると、「中」が全然なかったり、2回あったりする月が出てきそうです。
基本的に「中」の間隔の方が新月の周期よりも長いですから、「中」がない一ヶ月の方が、2回ある一ヶ月よりも数がずっと多いので、原則として「中」のない一ヶ月を「閏月」としよう、と定義しています。
閏月は、その前の月数に「閏」をつけて呼ばれます。たとえば、八月の次の月に「中」がない場合、次の一ヶ月は「閏八月」となるわけです。
| 新月 | 2月20日18時 | 二月一日 | |
| : | |||
| 春分 | 3月20日15時 | 二月三十日 | 二月中 |
| 新月 | 3月21日 7時 | 閏二月一日 | |
| : | |||
| 新月 | 4月19日22時 | 三月一日 | |
| 穀雨 | 4月20日 2時 | 三月二日 | 三月中 |
上の表をご覧ください。
2004年の春分は3月20日15時、穀雨が4月20日2時でした。
2月20日の新月から始まる一ヶ月は、「二月中」の「春分」を含みますから、旧暦の「二月」、4月19日の新月から始まる一ヶ月は、「三月中」の「穀雨」を含みますから、旧暦の「三月」となります。
となると、3月21日の新月から始まる一ヶ月は、「中」がないので月が決められません。そこでこの一ヶ月を「閏月」とし、「閏二月」と呼ぶわけです。
注意
これで、旧暦と呼ばれている暦について、計算できるようになりました。
ただし、これはあくまで原則です。最初に書いたとおり、世の中に出ている、たくさんの「旧暦」は、その編集した団体によって閏の入れ方などが違ってもおかしくはありません。どれが正しい、というのはナンセンスです。何しろ、公式な旧暦、というものは存在しないのですから。
この後、六曜や潮周りなどについても書くつもりでしたが、長くなってしまったので、別ページとしてまとめたいと思います。
