距離計のしくみ

写真を撮るとき、ピント合わせには、被写体までの距離を測る必要があります。

ものさしで測れない距離を測る

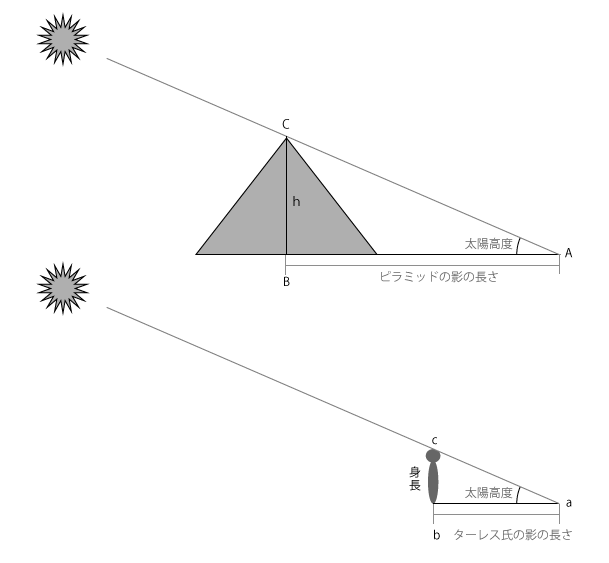
図１　ピラミッドの高さを求める。
太陽高度は一緒なので、影を作るものの高さと影の長さの比は同じ

一番簡単に、そして確実に距離を測る方法といえば、ものさしやメジャーなど、長さを測る道具を使うことです。机の上のものや家具、身長を測るのなら、それが一番でしょう。ただ、写真を撮るためにメジャーを取り出して腰を丸めて床にはわせて距離を測る、というのはスマートではありませんね。できるだけ簡単に距離が測れるようにしたいのです。

紀元前６世紀ごろのギリシャの哲学者タレスは、直接測るのは難しいピラミッドの高さを、自分とピラミッドの影の比から求めたといいます。タレスは、太陽の高さが同じであることを利用して、自分の身長と影の長さの比と、ピラミッドの高さと影の長さの比は同じだと考えました。右の図のピラミッドが作る三角形ABCと、タレス自身が作る三角形ａｂｃは、直角と太陽高度、２つの角の大きさが同じなので相似ですから、２つの三角形の辺の比、ＡＢ：ＢＣとａｂ：ｂｃは等しくなります。さすが現代にまで名前の残る哲学者、頭がいいです。

タレスは高さを測るために、このしくみを利用しましたが、縦ではなく、横にしてもかまわないはずです。

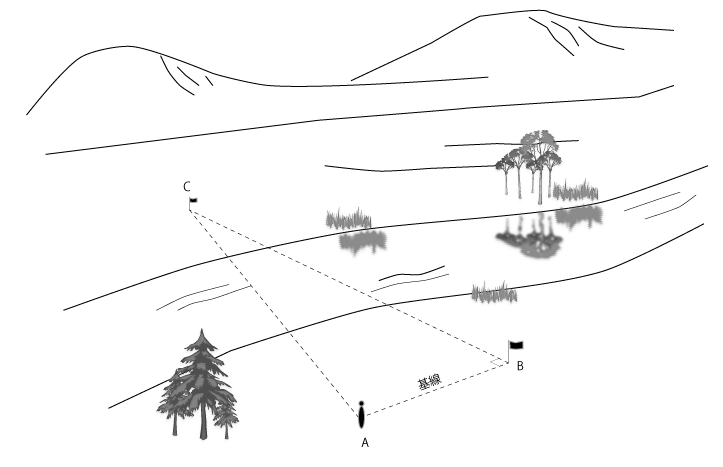
図２　川向こうまでの距離を測る

図２の、２本の旗の距離、こちら側の点Ｂから川向こうの点Ｃまでの距離を測りたいとします。タレスの方法で影の長さに当たるのが、川のこちら側AB間の距離。これは「基線」と呼ばれます。太陽高度に当たるのが、角Aの大きさです。

タレスは、もう一つの三角形、相似の三角形の辺の比からピラミッドの高さを求めましたが、今回は三角形は１つしかありません。でも大丈夫。工夫次第で、距離を図ることができるのです。

距離計のしくみ

距離計は、まさにこのしくみを使って距離を求めています（図３）

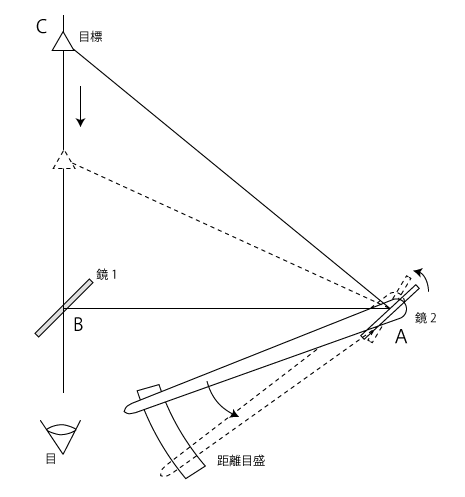
図３　距離計のしくみ

距離計も、タレスが考えた、三角形の「相似」の性質を用いていますが、「道具」としての改良がしてあり、三角形の角度や長さを数値で求める必要なく、「１辺の長さを固定し、２つの像を合わせる」という、機械的な方法で距離を求められるようにしています。

距離計には、２枚の鏡、もしくはプリズムがあり、A、Bのように、少し離して置いてあります。この、２枚の鏡やプリズムが反射した像を合わせることで距離を測っているのです。上の図２、風景の三角形と角をあわせると、鏡２というところがＡ、太陽高度の部分、鏡１が直角のＢ、目標がＣ。基線はＡＢ、求めたい距離はＢＣとなります。

しくみを詳しく説明していきましょう。

２枚の鏡のうち、鏡２は普通の鏡ですが、鏡１は半透明になっていて、この鏡を通して向こうの風景を見ることができます。目のところから、鏡１を通して目標を眺めると、目標と、鏡２で反射された風景が見えます。鏡２を回転できるようにしておくと、それを回すことで、鏡２でも同じ目標を映すことができ、目には目標が重なって見えます。このようにして、目標が重なる鏡２の角度を連動する針で示し、あらかじめ目盛に記録しておけば、鏡を回して像を重ねるだけで、目標までの距離が分かるようになります。

目標までの距離が分からないと、大砲を当てることができませんから、このしくみは昔の軍艦でも（もちろんもっと高度なものですが）使われていたそうです。

その精度は？

距離を測る機械、距離計を考えてみました。

ここで示したのは、「光学距離計」といいますが、この機械の素晴らしいところは、あらかじめ目盛をつけておく必要はあるものの、角度の数値を測らなくても、鏡に映った像をあわせることで距離を知ることができるところです。反対に、弱点としては、目標が遠くなると、鏡２の動く量が減りますから、精度が悪くなるところがあげられます。

光学距離計の精度は、目標までの距離の２乗に反比例し基線の長さに比例します。１ｋｍで１ｍの精度であっても、５ｋｍ離れると２５ｍの精度となり、遠くなるほど精度が悪くなっていきます。実際に使われたものは、精度を上げるために基線の長さを広く取り、それぞれの鏡のところに凸レンズをおいて、拡大した像で計測したそうですが、大掛かりになればなるほど運ぶのが大変で、しかも、理論的に精度を上げるのに限界がありますから、レーダーやGPSがある現在では、ほとんど使われなくなってしまったそうです。

それでも、三角形の１辺の長さと角度を測って、距離を求める、という考え方はシンプルで、分かりやすいものです。

はるか遠くのものを測るには向きませんが、この距離計、ちょっとした工作で作れそうですから、興味のある方は作ってみてはいかがでしょうか。この文章を書くのに参考にしたのも、子供向けの工作の本です¹。