三角比と年周視差

前のページ(距離計のしくみ)で、距離計という機械を使って距離を測る方法を紹介しました。今回はその続きです。

紙の上でなら、線の長さを測るのは難しくありません。地図を使えば、２点間の距離を求めることは簡単です。けれども、その地図を作るためには、遠くまでの距離を測らなければなりません。実際に地図を作る場合、２点間の距離を測る何らかの方法が必要で、前回、その道具のひとつ、距離計を紹介しました。

距離計は、三角形の「相似」という性質を利用して、１つの辺の長さと２つの角を使い、目標までの距離を求めます。その際、数値を測る必要がないように鏡を用いて機械的に求まるようにしてありましたが、逆に、楽に計算で求めるための工夫はできないものでしょうか。

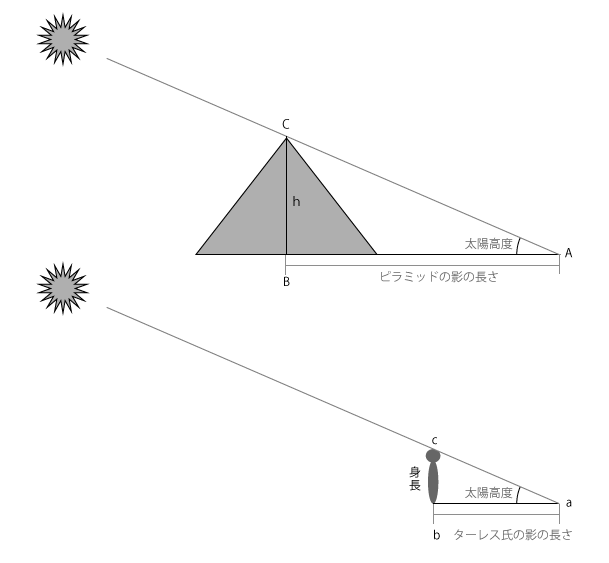
図１　ピラミッドの高さを求める（再掲）

もう一度、タレスの考えたことを使って考えてみましょう。

タレスは、ピラミッドと自分の影の長さ、自分の身長と太陽高度を使って、ピラミッドの高さを求めました。ピラミッドの三角形ABCと、タレスの三角形abcは相似。なので、２つの三角形の辺の比、AB：BCとab：bcは等しくなるのでした。これは、ピラミッドとタレスだけの関係ではありませんから、同じ太陽高度の時なら同じ比を使って、スフィンクスでも子供でも電信柱でもスカイツリーでも、影の長ささえ測れば、その高さを求められます。

これは、三角形の辺の比なので、「三角比」と呼ばれます。これで数学が嫌いになる人が多い、とか噂される、sin、cos、tanというやつです。ここで用いている関係はタンジェント(tan)にあたります。タンジェントとか言うと難しく感じてしまうかもしれませんが、要は２辺の比、対辺と底辺の割り算を一つの記号にしたもの。右のピラミッドの三角形で言えば、角Aに対応する辺の比AB:BC、対辺BCを底辺ABで割ったものを、tanAという記号で表そうということです。

です。

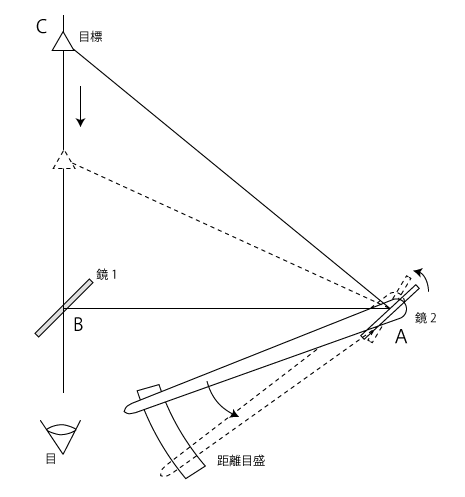
図２　距離計のしくみ（再掲）

距離計が作る三角形でも同じ関係、右の図では、対辺BCが目標までの距離、底辺ABが基線にあたります。タレスが求めたいピラミッドの高さ、距離計で求めたい目標までの距離は、辺BCです。今分かっているのは、角Aの角度と辺ABの長さ。\(\eqref{no1}\)を変形して、

とすることで、ピラミッドの高さも目標までの距離も計算で求めることができます。

tanAは、Excelなどの表計算ソフトや関数電卓で計算できますし、三角関数表で調べることもできます。

三角比、sin、cos、tanは、三角形の１角の角度と１辺の長さから、他の辺の長さや角の角度を求める道具。こうして、三角比を求めておけば、直角三角形の関係にある１つの角度と１つの辺の長さで、どんなに遠いところでも距離を求めることができます。Excelや関数電卓で使える三角関数は、こうして、三角比を関数にしたものです。

ちなみに、tanAという表記に慣れない場合、何を計算しているのかが分かりづらいかもしれませんが、\(\eqref{no2}\)のtanAに、\(\eqref{no1}\)を代入してみれば、

という、当たり前の関係になります。

視差

さて、２回にわたって、三角形を使って距離を求める話をしてきましたが、ここは天文のサイト、ここからは星の話題。

もうお分かりでしょうが、今、紹介した距離の求め方は、そのまま、恒星の距離を求める方法として使われています。

地球上の地図と同じように、宇宙空間でも星の分布、恒星の地図はとても重要です。けれども「天球」という言葉があるように、星は空に球状に張り付いているように見え、星までの距離はどれくらいなのか、見当もつきません。

顔の前に人差し指を立て、右目と左目交互につぶって人差し指を見ると、背景に対して人差し指が動いて見える、という実験をしたことがある人も多いと思います。これは「視差」と呼ばれますが、私たちは、この視差から、顔の前の人差し指はもちろん、テレビ、家の前の電柱、遠くの工場の煙突、はるかかなたに見える富士山、目に見えるすべてのものの距離を視覚として感じています。

そして、視差は両目の幅だけではなく、私たちが見る場所を変えることで、さらに遠くの距離感を教えてくれます。月夜に歩いているとき、周りの風景は変わっても、月はいつまでもついてくるように感じる、それも視差。周りの風景の移動による視差は大きく、月ははるか遠くにあるので、移動をしても、見える場所が変わらない、視差が小さいのです。

昔の人々は天動説を信じていたといわれますが、地球は動かない、という根拠として、古代ギリシャの時代から、この視差をあげています。もし、地球が宇宙の中心でなく動いているのなら、地球の移動によって星の位置は変化するはずだ、しかし、変化は見られないのだから、地球は動かず、太陽や惑星が地球の周りを回っているのだ、というわけです。確かに、１年間に目で見て分かるほど、星の位置は変化しません。それどころか、ふつうの望遠鏡を使っても分かりません。

年周視差

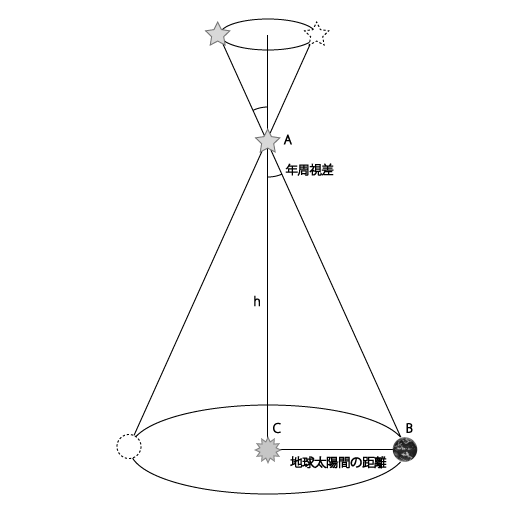
図３　年周 視差

けれども、実際には、地球が太陽の周りを回る、その見る場所の移動で、恒星の位置もごくわずかですが変化しています。これは、地球が太陽の周りを公転するために起こる視差なので「年周視差」と呼んでいます。

年周視差は、古代ギリシャから２０００年近くの間、観測することはできませんでした。人類の歴史から見てつい最近の１９世紀、天体観測技術が向上し恒星の位置を角度の０．１秒という単位で測れるようになって、ようやく年周視差が観測されたのです。この角度を測ったのは、ドイツの天文学者ベッセル。はくちょう座６１番星という、固有運動の動きの早い星に注目し、その視差、０．３１４秒を求めました。０．３１４秒は、東京タワーのてっぺんから、シャープペンの芯を見るようなもの。古代ギリシャの技術では、とても観測できるようなものではなかったのです。

年周視差の解説図が右。太陽の周りを地球が公転し、見る場所が変わることで、星も位置を変えて見えます。太陽と地球と星、これを直角三角形にして、星の位置の変化角度が年周視差というわけです。年周視差が観測できれば、太陽・地球・恒星で作る直角三角形の、ひとつの角の角度と、地球と太陽間、１つの辺の長さが分かっていますから、三角比を使うことで、恒星までの距離が計算で求められます。

身近な、カメラの被写体までの距離を測るのと、はるか宇宙の星の距離を測るのは、スケールが違うだけで、同じ相似の三角形を使う、同じ考え方なのですね。

では、このベッセルの求めた数字から、はくちょう座６１番星までの距離を求めてみましょう。

現在の値は１１．４光年ですから、ほぼ、今と変わらない数値が求まったのです。

こうして、恒星までの距離を直接求めることができるようになりました。

この方法、遠くのものを測るときは誤差が大きくなる、という話を、「距離計のしくみ」でもお話しました。星の場合、年周視差でも約０．７秒強しかありません。このサイトで使っているヒッパルコスカタログの観測精度でも、せいぜい数百光年の範囲が限界で、何千光年という距離は測ることはできないのです。

観測精度が上がれば、直接距離を求めることができる範囲も広がります。日本のＪＡＳＭＩＮＥ ¹、ヨーロッパのＧaia ²など、宇宙空間から星までの距離を測る計画が進められていますが、それでも、宇宙はまだまだ広く、ＧＡＩＡでも、直接視差が観測できるのは銀河系の半分くらい、３万光年くらいです。

では、何十億光年かなたの銀河までの距離、どうやって求めたのでしょうか。それはこれからご紹介しましょう。