ホーム　≫　星空ガイド　≫　過去未来の星座のこと　≫　過去・未来の星空　計算の方法

パルディ天球図　より、こと座　Ignace Gaston Pardies, Wikimedia Commons

過去・未来の星空　計算の方法

「過去未来の星空」コンテンツでは、かなり長い期間の恒星の運動を調べています。

どうやって計算しているのだろう、と興味のある方もいらっしゃるかと思いますので、ここにまとめてみました。

ここでの計算の大前提として、恒星は等速直線運動をしていることとします。実際には、星はすべて銀河系を公転していますから、直線ではなく楕円運動をしているでしょうし、恒星間の引力の働きもあると思います。ただ、現在から前後１００万年という期間では、等速直線運動とみなしてよいのではないかと考えます。

銀河系の重力の影響を含めて計算している天文学者の方たちもいらっしゃいます。その結果と比べても大きく異なる結果は出ていないので、ここでの計算方法も、近似値として十分に使えると思います。

星の固有運動

遠い過去・未来の星空を調べるためには、星ひとつひとつがどのように動いているか、を、知る必要があります。これを「固有運動」と呼び、ひとつひとつの星の固有運動を計算できれば、過去・未来の星空を知ることができます。星の固有運動を計算する、といっても、特に難しいことはなく「時速１０００キロメートルで南に向って飛んでいる飛行機は、２時間後には何キロメートル先にありますか？」という問題と本質は同じ。

算数の問題と違うところは、最初の「時速１０００キロメートルで南に」という部分も観測によって調べなければならないところですが、現在では、過去未来の星空を計算するためにそこから始める必要はありません。天文台で観測した結果が、星のカタログ＝星表にまとめられています。

すべての星表に掲載されているわけではありませんが、位置や明るさ、スペクトルなどのほかに、固有運動に関わるデータを掲載しているものがあります。

星表に掲載されている、過去未来の星の位置の計算に必要な情報は、

  • 星の位置　　　　　　　\(\alpha\) 　　\(\delta\)　　　　赤径、赤緯
  • １年間の固有運動量　　\(\mu\alpha\) 　\(\mu\delta\)　　　地球から見た星の動き
  • 視線速度　　　　　　　\(R0\)　　　　　　近づいてきているか、離れていっているかの速度
  • 年周視差　　　　　　　\(\pi\)　　　　　　　その星までの距離

この４つ。

これらを使えば、過去未来の星空を知ることができます。では、その方法を紹介していきましょう。

固有運動の簡単な求め方

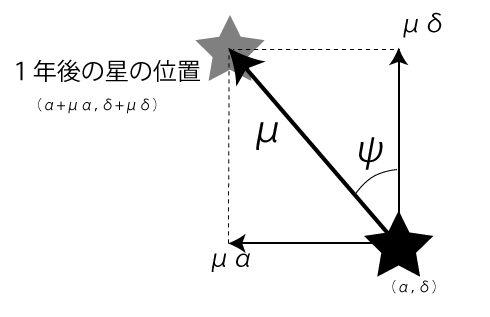
図１　固有運動量

図１　固有運動量

上の4つの要素を見ると、そのものずばり「固有運動」量というものがあります。これは、まさに星の動きの量、地球から見て１年間に動いた量を示しています。これを使えば、星の動きを求めることができます。

星表に出ている固有運動量は一般的に、赤径（\(\mu\alpha\)）＝横に動いた量、赤緯（\(\mu\delta\)）＝縦に動いた量、の２つの要素に分けて掲載されています。

星の位置も、地球上の位置と同じで座標で表し、地上で言う経度が赤径、緯度が赤緯にあたります。現在の星の位置は主に、赤径・赤緯の二つの数値で示していますから、そのそれぞれに\(\mu\alpha\)（赤径分の移動量）、\(\mu\delta\)（赤緯分の移動量）を、必要な年数分、足してあげれば、その星の過去未来の位置が計算できます。

　　　過去未来の赤径　＝　現在の赤径\(\alpha\)　＋　\(\mu\alpha\)（赤径）　×　年数
　　　過去未来の赤緯　＝　現在の赤緯\(\delta\)　＋　\(\mu\delta\)（赤緯）　×　年数
　　　年数は、未来はプラス、過去ならマイナスです

この式でも、そう遠くない過去未来なら、星の位置を知ることができます。掛け算と足し算だけですから、本当に簡単に求めることができます。

けれども、何万年、何十万年という話になると、これではよろしくありません。

というのは、上の計算で使った\(\mu\alpha\)（赤径）、\(\mu\delta\)（赤緯）は、地球から見た、現在の動く方向、そして速さだからです。星が空に張り付いている、という前提の式で、あくまでも近似式です。星は、私たちと同じ３次元を運動していますから、天球に映った星の動きを使ったのでは、正しい計算はできません。

正面から飛行機がこちらに向かってくるところを想像してみてください。遠くに見えているときは、位置はあまり変わらずにゆっくり動いているように見えます。近づくにつれてどんどん速くなり、頭上を通過するときには、あっという間に後へと位置が変わり、遠ざかるとともにまた、位置は変わらずゆっくり動いているように見えるでしょう。まっすぐ飛んでいれば、進む向きが変わって見えることはありませんが、同じ速さで飛んでいても、地上からでは速さはずいぶん変わって見えます。この飛行機の動きを「遠くにあるころの動き」「頭上を通過するときの動き」など、その瞬間に見えた速さだけを基にしては、正しく知ることができない、ということです。見えた動きから、飛行機の実際の速さを調べて、それを基にして見える位置を計算しなければ、間違った答えになってしまいます。星も、おなじこと。星の動きを長期間調べるには、星の実際の速さを知る必要があるのです。

全固有運動量と、固有運動の向き

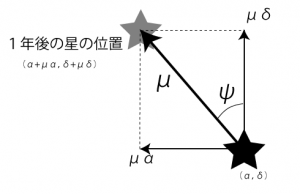
図１　固有運動量（再掲）

図１　固有運動量（再掲）

もう一度、図１を見てください。図にある\(\psi\)（プシー、プサイ）と\(\mu\)（ミュー）は、地球から見た固有運動の向きと速さです。これからの計算のために、この２つを求めます。

固有運動に関する情報は\(\mu\alpha\)と\(\mu\delta\)。観測で知ることができた、赤径赤緯それぞれの固有運動量を「速さ」と「動いていく方向」に分けなおします。

まずは、固有運動の向き\(\psi\)を求めてみましょう。固有運動の向き\(\psi\)は、天の北極、北を０度として、東→南→西と３６０度まで測ります。直角三角形なので、三角比を使って、

\[ \begin{align} \psi&=tan\left(\frac{\mu\alpha}{\mu\delta}\right)\\[14pt] &（\mu\delta \gt 0　で、I、IV象限、 \mu\delta \lt 0 でII、III象限）\\[14pt] \end{align} \]

として求めます。

「星が直線運動をしている」という前提で計算していますから、この値はこのまま最後まで使います。

次に、１年間の地球から見た固有運動の速さ、全固有運動量\(\mu\)は、\(\mu\alpha\)と\(\mu\delta\)をあわせたもの。

\[ \begin{align} \mu=\sqrt{\mu \alpha^{2} + \mu \delta^{2}}\\[14pt] \end{align} \]

として求めます。

宇宙空間での星の動き

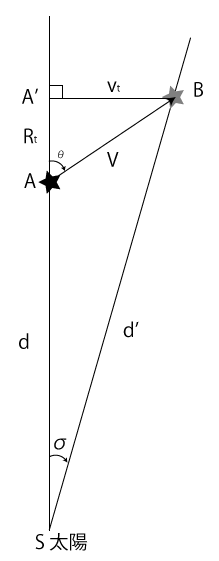
図２　恒星運動の角距離

図２　恒星運動の角距離

つづいて図２。上で示したデータを使って星の動きの計算方法を調べていきましょう。

始め、恒星は\(A\)にいました。そして、時間が過ぎて\(t\)年後、\(B\)までやってきました、という図です。これは、地球から眺めたのではなく、宇宙空間から見ています。\(A\)から\(B\)に動いた、という動きは、宇宙空間でのもの。

宇宙空間で\(t\)年間かけて星は\(A\)から\(B\)へと動きましたが、この動きを地球から眺めていると、\(S\)（太陽）と書かれている点の角\(\sigma\)（シグマ）分、動いたように見えるはずです。これを角距離\(\sigma\)と呼びます。

これが\(t\)年間ではなく、１年間ということであれば、先ほど求めた全固有運動量\(\mu\)と同じです。最初に紹介した簡単な固有運動の計算方法は、\(\sigma\)を求めるのに、この\(\mu\)を単純に\(t\)倍していたことになりますが、それが問題だったわけです。正確にするには、宇宙空間での実際の星の運動を考えなければなりません。

この角距離\(\sigma\)が分かれば、恒星が進む方向は\(\psi\)で分かっていますから、\(t\)年後には恒星がどこにいるか、が分かります。

ただ、この\(\sigma\)は、最初に提示した４つのデータの中にはありませんから、ちょっと工夫をしないといけません。

図を見ると、\(AB\)を結んでいる\(V\)というのが、実際の宇宙空間での\(t\)年間の星の動き。これを知りたいのですが、ここで\(V\)の代わりに、奥行き\(R\)と横向き\(V\)、ふたつの要素に分けて考えてみます（図では、\(t\)年間の動きなので、\(Rt\)、\(Vt\)となっています）　というのは、奥行き方向の速度\(R\)、これは視線速度と呼ばれ、観測で求められているからです。最初に提示した４つの情報のひとつ、星表に[ｋｍ／ｓ]単位で掲載されています。このデータから、視線方向の星の動きは計算できます。

もうひとつの横向き方向の速度\(V\)、これは接線速度と呼ばれ、こちらは残念ながらデータにありませんので、計算で求めないといけません。この計算には、全固有運動量\(\mu\)ともうひとつ、年周視差\(\pi\)を使います。

ちょっと頭の体操を。

視線速度、接線速度

ではさっそく、接線速度の計算式を考えましょう。図３の三角形を使います。図２と同じですが、補助線の引き方が違っています。また、\(AB\)は\(t\)年間ではなく１年間の動き、とします。\(t\)年間の動きの計算のために、１年間の量を求めるのです。

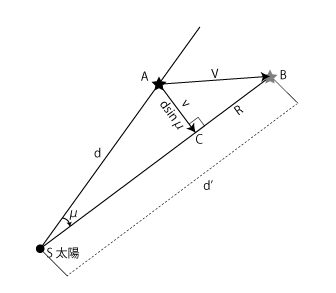
図３　視線速度　接線速度

図３　視線速度　接線速度

三角形\(ACS\)は直角三角形です。なので、三角比の定義から、接線方向の移動量\(AC\)は、地球と恒星の距離\(d\)に、\(sin(\mu)\)を掛けたもの。

\[ \begin{align} AC = d sin(\mu) \tag{1} \label{no1} \\[14pt] \end{align} \]

\(\mu\)は角度ですから、星までの距離が決まらないと、移動量も距離の単位では求まらないということです。同じ角度の１度の動きでも、近ければゆっくりでしょうし、うんと遠ければうんと早いでしょう。

\(AC\)を求めるには、星までの距離\(d\)を決めてあげないといけませんが、ここで、

\[ \begin{align} sin(\pi) = \frac{a}{d} \tag{2} \label{no2} \\[14pt] \end{align} \]

という式を提示します。これは、年周視差\(\pi\)を求める式。\(a\)は 地球軌道半径、\(d\)は恒星までの距離。地球軌道半径\(a\)を、恒星までの距離\(d\)で割ったものが、地球の公転運動によって動いて見える恒星の角度 = 年周視差、ということです。

年周視差\(\pi\)から星までの距離\(d\)を求めるには、\(\eqref{no2}\)式を変形して

\[ \begin{align} d = \frac{a}{sin(\pi)} \tag{3} \label{no3} \\[14pt] \end{align} \]

\(\eqref{no1}\)に代入すると、

\[ \begin{align} AC = a \times \frac{sin(\mu)}{sin(\pi)} \tag{4} \label{no4} \\[14pt] \end{align} \]

これで、１年間の接線方向の移動量\(AC\)=視線速度\(v\)を求めることができます。

これを[ｋｍ／ｓ]単位の接線速度にするには、地球軌道半径\(A\)［ｋｍ］を、１年間の秒数\(n\)で割って、

\[ \begin{align} 接線速度　v　&=　AC　=　\frac{a}{n} \times \frac{sin( \mu ) }{sin( \pi) }［ｋｍ／ｓ］ \\[14pt] 地球軌道半径　a &= 149,600,000［ｋｍ］\\[14pt] １年間の秒数　n &= 86,400 \times 365.2422 = 31,560,000［ｓ］　より、\\[14pt]\\[14pt] \frac{a}{n}　&= \frac{149,600,000}{31,560,000}　=　4.741［ｋｍ／ｓ］\\[14pt] 　なので、 接線速度　v &= \frac{a}{n} \times \frac{sin(\mu)} {sin( \pi )} = 4.741 \times \frac{sin( \mu )}{sin(\pi)} ［ｋｍ／ｓ］\\[14pt] \end{align} \]

と、求まりました。

でも、ちょっと待ってください。今、そもそも何を計算したいのか、というと、何千年、何万年という過去未来の星の位置です。それを［ｋｍ／ｓ］といった単位で計算しても、どのみち［光年／年］や、［パーセク／年］に変換する必要がでてくるでしょう。接線速度の単位は、今の\(\displaystyle \frac{a}{n}\)の単位で決まりますから、時間の単位は[年]　距離の単位は[光年]で計算することにしましょう。

式\(\eqref{no4}\)の場合、時間は始めから１年間として計算していますから\(n\)は１［年］、地球軌道半径\(a\)を、１光年を［ｋｍ］単位で表した9,460,000,000,000［ｋｍ］で割って、

\[ \begin{align} a &= \frac{149,600,000［ｋｍ］}{9,460,000,000,000［ｋｍ］} = 0.000001581 \\[14pt] v［光年／年］&= 0.000001581 \times\frac{sin(\mu)}{sin(\pi)} \tag{5} \label{no5} \\[14pt] \end{align} \]

とします。

あわせて視線速度も[光年／年]に変換しておきましょう。元々が[ｋｍ／ｓ]ですから、１年間の秒数を［ｋｍ］単位の１光年で割ったものを掛けてあげればよく、

\[ \begin{align} \frac{31,560,000}{9,460,000,000,000} &= 0.000003336\\[14pt] R［光年／年］&=　0.000003336 \times R\\[14pt] \end{align} \]

これで、接線速度、視線速度ともに[光年／年]単位で求めることができました。1

\(\sigma\)を求める

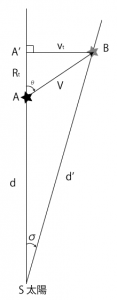
図２　恒星運動の角距離(再掲)

図２　恒星運動の角距離(再掲)

上で、［光年／年］単位の視線速度\(R\)、接線速度\(V\)が求まりました。これらを使って\(t\)年間の角距離\(\sigma\)を求めます。

再び図２です。

直角三角形\(BA’S\)で、三角比の定義より、

\[ \begin{align} d’sin(\sigma) &= A’B\\[14pt] d’cos(\sigma) &= (d + AA’)\\[14pt] \end{align} \] \(A’B\) は、t年間の視線方向の移動距離 = \(v \times t\) \(AA’\) は、t年間の視線方向の移動距離 = \(R \times t\)

なので、

\[ \begin{align} 　d’sin(\sigma) &= v \times t\tag{6-1} \label{no6-1} \\[14pt] 　d’cos(\sigma) &= (d + R \times t) \tag{6-2} \label{no6-2} \\[14pt] \end{align} \]

となります。このふたつの式から、\(t\)年間の角距離\(\sigma\)と、\(t\)年後の太陽系からの距離\(d’\)を求めることができます。

\(tan(\sigma) = \displaystyle \frac{sin(\sigma)} {cos(\sigma)}\)より、\(\eqref{no6-1}\)式の値を\(\eqref{no6-2}\)の値で割り、\(tan(\sigma)\)の値から\(\sigma\)を求めます。\(\eqref{no6-1}\)、\(\eqref{no6-2}\)式の符号で、どの象限かがわかるわけです。

求めた\(\sigma\)で、たとえば\(cos(\sigma)\)を計算して、\(\eqref{no6-2}\)の値を割れば、\(d’\)も求まります。単位は［光年］です。

ここまで長かったですが、\(t\)年間の恒星の移動角距離\(\sigma\)がようやく求まりました。\(\sigma\)と固有運動の向き\(\psi\)を使って、\(t\)年後の恒星の位置を計算しましょう。

固有運動で星を動かす

ここからは、球面三角法という、球面上の「正弦法則」「余弦法則」などを使って、天球上で星がどう動くのかを計算します。が、球面三角法は複雑で、説明が長くなりますので、答えだけをここに出しましょう。

\(t\)年後の星の位置を求めるために使うデータは、現在の星の位置\(\alpha\)、\(\delta\)、固有運動方向\(\psi\)、そして今求めた\(t\)年間の移動角距離\(\sigma\)です。\(t\)年後の星の位置は、\(\alpha’\delta’\)で表してあります。

\(\eqref{no7-1}\)式や\(\eqref{no7-2}\)式の\(\alpha’-\alpha\)は、これでひとつの未知数、現在の赤径との差を表し、\(\alpha’\)から\(\alpha\)を引く、という意味ではありません。ばらして別々に計算したりしないようにしてください。

\[ \begin{align} 　cos(\delta’) sin(\alpha’-\alpha) &= sin(\sigma) sin(\psi)\tag{7-1} \label{no7-1} \\[14pt] 　cos(\delta’) cos(\alpha’-\alpha) &= cos(\delta) cos(\sigma) – sin(\delta) sin(\sigma) cos(\psi)\tag{7-2} \label{no7-2} \\[14pt] 　sin(\delta’) &= sin(\delta) cos(\sigma) + cos(\delta) sin(\sigma) cos(\psi)\tag{7-3} \label{no7-3} \\[14pt] \end{align} \]

まず、\(\eqref{no7-1}\)で求めた数値を\(\eqref{no7-2}\)で求めた数値で割ってtan\(\alpha’-\alpha\)にし、象限判断をして赤径の移動量\(\alpha’-\alpha\)を求めます。

現在位置からの移動量なので、現在位置の赤径\(\alpha\)に、求めた\(\alpha’-\alpha\)を足して、\(t\)年後の赤径が計算できます。

\(t\)年後の赤緯\(\delta’\)は、９０から－９０の範囲なので、象限判断は不要で、\(\eqref{no7-3}\)式からそのまま計算できます。

まとめ

これで、\(t\)年後の星の位置が計算できるようになりました。天文計算の中では簡単なものですが、恒星の数が多くなると、計算は面倒です。

このサイトで使っている星図は、自作の計算・描画プログラムを使用して作成しています。

最後に、この計算に必要な式をまとめておきましょう。

固有運動計算に必要なデータ

  • 星の位置　　　　　　　\(\alpha\) 　　\(\delta\)　　　　赤径、赤緯
  • １年間の固有運動量　　\(\mu\alpha\) 　\(\mu\delta\)　　　地球から見た星の動き
  • 視線速度　　　　　　　\(R0\)　　　　　　近づいてきているか、離れていっているかの速度
  • 年周視差　　　　　　　\(\pi\)　　　　　　　その星までの距離\(\\[14pt]\)

固有運動方向\(\psi\)全固有運動量\(\mu\)

\[ \begin{align} \mu&=\sqrt{\mu \alpha^{2} + \mu \delta^{2}}\\[14pt] \psi&=tan\left(\frac{\mu\alpha}{\mu\delta}\right)\\[14pt] &（\mu\delta \gt 0　で、I、IV象限、 \mu\delta \lt 0 でII、III象限）\\[14pt]\\[14pt] \end{align} \]

視線速度\(R\)、接線速度\(v\)

\[ \begin{align} R &=　0.000003336 \times R0\\[14pt] v &=　0.000001581 \times\frac{sin(\mu)}{sin(\pi)}\\[14pt]\\[14pt] \end{align} 単位は[光年／年] \]

距離角\(\sigma\)　移動後の距離\(d’\)

計算期間\(t\)は、年を単位とする
現在の距離\(d = \displaystyle\frac{a} {sin(\pi)}　　　a = \frac{149,600,000［ｋｍ］} {946,000,000,0000［ｋｍ］} \)として、 \[ \begin{align} \\[7pt] 　d’sin(\sigma) &= v \times t\\[14pt] 　d’cos(\sigma) &= (d + R \times t) \\[14pt] 　tan(\sigma) &= \frac{d’sin(\sigma)}{d’ cos(\sigma)}\\[14pt] 　d’ &= \frac{d’ cos(\sigma)} {cos(\sigma)}\\[14pt]\\[14pt] \end{align} \]

\(t\)年後の恒星の位置\(\alpha’\delta’\)

\[ \begin{align} 　cos(\delta’) sin(\alpha’-\alpha) &= sin(\sigma) sin(\psi) \\[14pt] 　cos(\delta’) cos(\alpha’-\alpha) &= cos(\delta) cos(\sigma) – sin(\delta) sin(\sigma) cos(\psi) \\[14pt] 　sin(\delta’) &= sin(\delta) cos(\sigma) + cos(\delta) sin(\sigma) cos(\psi) \\[14pt] &(\alpha’ – \alpha)は、現在との差なので注意\\[14pt] \end{align} \]
[天文計算入門　P112-116　　天体の位置計算 P43-46]
  1. ↩こんな小さい数字ばかりで、アンダーフローしない？　と気にされる方もいらっしゃるでしょう。パソコンであれば、浮動少数で有効数字は確保できてますし、乗算で使う数値なので、桁落ちは起きません。逆にkm/s単位では、オーバーフローは？という話にもなりますね