
サロス周期とメトン周期
2010年は、月食が3回も見られた年でした1 。千葉では天気が悪く、最初のものしか見ることができませんでしたが。
そう言われても、へーそうですか、という反応が普通の人だと思いますが、実は結構珍しいことなのです。1年間に3回月食が見られるのは、次は2094年、実に84年後! と書いても、だから何? と言われそうですね。
では、ちょっとアブナイ系の話をすると、2010年に起きた3回の月食の日付は、1月1日、6月26日、12月21日と、シンメトリカルになっているのです。元日に月食、しかも日付がシンメトリカル、昔なら「不吉」とか言われそうな偶然です。
全部が皆既月食であれば、いよいよアヤシイ話になってきますが、2010年に見られた皆既月食は1回。残りの2回は部分月食でした。残念。
月食の秘密
アブナイ系の話はこれくらいにして、まじめな話に戻します。偶然と一緒にしてはいけませんが、月食、そして日食には、ちょっとミステリーっぽい数字があります。今回は、それについて調べてみましょう。
まずは、下の表をご覧ください。
| 期間 | 回数 | 期間 | 回数 |
|---|---|---|---|
| 1950年代 | 4回 | 2010年代 | 7回 |
| 1960年代 | 5回 | 2020年代 | 7回 |
| 1970年代 | 6回 | 2030年代 | 6回 |
| 1980年代 | 7回 | 2040年代 | 6回 |
| 1990年代 | 4回 | 2050年代 | 4回 |
| 2000年代 | 5回 | 2060年代 | 6回 |
東京で見られる月食の回数を、10年ごとにまとめたものです。月食の見られる回数は、意外と増減していることが分かります。多くて7回、少なくて4回。2020年代の皆既月食は、7回見られます。
続いてこの表。
| 日時 | 離角 | 種類 | 日時 | 離角 | 種類 | 日時 | 離角 | 種類 |
|---|---|---|---|---|---|---|---|---|
| 1981/01/20 16:50 | 0゚59′ | 部分 | 1999/02/01 01:17 | 0゚59′ | 部分 | 2017/02/11 09:43 | 0゚60′ | 部分 |
| 1981/07/17 13:47 | 0゚39′ | 部分 | 1999/07/28 20:33 | 0゚44′ | 部分 | 2017/08/08 03:20 | 0゚48′ | 部分 |
| 1982/01/10 04:56 | 0゚18′ | 皆既 | 2000/01/21 13:43 | 0゚18′ | 皆既 | 2018/01/31 22:29 | 0゚18′ | 皆既 |
| 1982/07/06 16:31 | 0゚03′ | 皆既 | 2000/07/16 22:56 | 0゚02′ | 皆既 | 2018/07/28 05:22 | 0゚06′ | 皆既 |
| 1982/12/30 20:29 | 0゚23′ | 皆既 | 2001/01/10 05:20 | 0゚23′ | 皆既 | 2019/01/21 14:12 | 0゚23′ | 皆既 |
| 1983/06/25 17:23 | 0゚45′ | 部分 | 2001/07/05 23:55 | 0゚40′ | 部分 | 2019/07/17 06:31 | 0゚35′ | 部分 |
| 1984/11/09 02:55 | 0゚60′ | 部分 | 2002/11/20 10:46 | 1゚01′ | なし | 2020/11/30 18:42 | 1゚02′ | なし |
| 1985/05/05 04:56 | 0゚21′ | 皆既 | 2003/05/16 12:40 | 0゚25′ | 皆既 | 2021/05/26 20:18 | 0゚29′ | 皆既 |
| 1985/10/29 02:42 | 0゚22′ | 皆既 | 2003/11/09 10:18 | 0゚23′ | 皆既 | 2021/11/19 18:02 | 0゚25′ | 皆既 |
| 1986/04/24 21:42 | 0゚23′ | 皆既 | 2004/05/05 05:30 | 0゚19′ | 皆既 | 2022/05/16 13:11 | 0゚15′ | 皆既 |
| 1986/10/18 04:18 | 0゚18′ | 皆既 | 2004/10/28 12:04 | 0゚16′ | 皆既 | 2022/11/08 19:59 | 0゚14′ | 皆既 |
| 1986/10/07 13:01 | 1゚00′ | 部分 | 2005/10/17 21:03 | 0゚58′ | 部分 | 2023/10/29 05:13 | 0゚56′ | 部分 |
| 1988/03/04 01:12 | 0゚54′ | 部分 | 2006/03/15 08:47 | 0゚55′ | 部分 | 2024/3/25 16:13 | 0゚57′ | なし |
| 1988/08/27 20:04 | 0゚53′ | 部分 | 2006/09/08 03:51 | 0゚57′ | 部分 | 2024/09/08 11:43 | 1゚00′ | 部分 |
| 1989/02/21 00:35 | 0゚16′ | 皆既 | 2007/03/04 08:20 | 0゚17′ | 皆既 | 2025/03/14 15:58 | 0゚19′ | 皆既 |
| 1989/08/17 12:07 | 0゚09′ | 皆既 | 2007/08/28 19:37 | 0゚13′ | 皆既 | 2025/09/08 03:11 | 0゚16′ | 皆既 |
| 1990/02/10 04:10 | 0゚24′ | 皆既 | 2008/02/21 12:25 | 0゚23′ | 皆既 | 2026/03/03 20:33 | 0゚22′ | 皆既 |
| 1990/08/06 23:11 | 0゚36′ | 部分 | 2008/08/17 06:09 | 0゚32′ | 部分 | 2026/08/28 13:12 | 0゚28′ | 部分 |
| 1991/12/21 19:32 | 0゚59′ | 部分 | 2010/01/01 04:21 | 0゚60′ | 部分 | 2028/01/12 13:12 | 0゚60′ | 部分 |
| 1992/06/15 13:56 | 0゚35′ | 部分 | 2010/06/26 20:37 | 0゚39′ | 部分 | 2028/07/07 03:18 | 0゚44′ | 部分 |
| 1992/12/10 08:43 | 0゚18′ | 皆既 | 2010/12/21 17:15 | 0゚19′ | 皆既 | 2029/01/01 1:50 | 0゚19′ | 皆既 |
| 1993/06/04 21:59 | 0゚10′ | 皆既 | 2011/06/16 05:11 | 0゚05′ | 皆既 | 2029/06/26 12:21 | 0゚01′ | 皆既 |
| 1993/11/29 15:25 | 0゚22′ | 皆既 | 2011/12/10 23:30 | 0゚21′ | 皆既 | 2029/12/21 07:40 | 0゚21′ | 皆既 |
| 1994/05/25 12:29 | 0゚55′ | 部分 | 2012/06/04 20:02 | 0゚50′ | 部分 | 2030/06/16 03:32 | 0゚46′ | 部分 |
| 1995/04/15 21:17 | 0゚58′ | 部分 | 2013/04/26 05:07 | 1゚01′ | 部分 | 2031/05/07 12:50 | 1゚04′ | なし |
| 1996/04/04 09:09 | 0゚14′ | 皆既 | 2014/04/15 16:45 | 0゚17′ | 皆既 | 2032/04/26 00:12 | 0゚20′ | 皆既 |
| 1996/09/27 11:54 | 0゚21′ | 皆既 | 2014/10/08 19:54 | 0゚23′ | 皆既 | 2032/10/19 04:01 | 0゚25′ | 皆既 |
| 1997/03/24 13:39 | 0゚27′ | 皆既 | 2015/04/04 20:59 | 0゚24′ | 皆既 | 2033/04/15 04:11 | 0゚21′ | 皆既 |
| 1997/09/17 03:46 | 0゚23′ | 皆既 | 2015/09/28 11:46 | 0゚20′ | 皆既 | 2033/10/08 19:54 | 0゚18′ | 皆既 |
| 凡例 | ||||||||
| 見られない(地平線下) | 月食中に沈む(月没帯食) | 月食中に昇る(月出帯食) | ||||||
この表は、1980年から2033年までに起こる月食をまとめたものです。皆既月食、部分月食と問わず、日本から見えないものも含まれています。白い枠のものが東京で最初から最後まで見られるもの、灰色の枠のものが見えません。他の色付きは凡例を見てください。
さて、2010年はと見ると、1月1日部分、6月26日部分、12月21日皆既、ただしピンク色枠なので、月出帯食(月が欠けたまま昇ってくる月食)です。確かに3回起こります。
でも、この表見づらいよ
ところで、この表、なんだか変な風に組んであります。90年代、00年代とか区切っている割にはその途中で改列しているし、「なし」という、月食が起こらない日も入っているし、しかも2033年なんて中途半端なところで終わっているし。
実はこの表、ある法則に基づいて作ってあります。ヒントは横1列の日付です。たとえば、
| 日時 | 離角 | 種類 | 日時 | 離角 | 種類 | 日時 | 離角 | 種類 |
|---|---|---|---|---|---|---|---|---|
| 1991/12/21 19:32 | 0゚59′ | 部分 | 2010/01/01 04:21 | 0゚60′ | 部分 | 2028/01/12 13:12 | 0゚60′ | 部分 |
| 1992/06/15 13:56 | 0゚35′ | 部分 | 2010/06/26 20:37 | 0゚39′ | 部分 | 2028/07/07 03:18 | 0゚44′ | 部分 |
| 1992/12/10 08:43 | 0゚18′ | 皆既 | 2010/12/21 17:15 | 0゚19′ | 皆既 | 2029/01/01 1:50 | 0゚19′ | 皆既 |
| 見られない(地平線下) | 月食中に沈む(月没帯食) | 月食中に昇る(月出帯食) | ||||||
隣同士の間隔が、18年と10日前後と8時間くらいずれています。ほかの列もすべてそうなっているのがわかりますか?
また、「離角」欄にも注目です。ここでいう離角は、地球の影の中心と月との距離のことです。離角を横1列でみると、これもほぼ同じくらいの値になっています。
月食は、月が地球の影に入って起こる現象ですから、地球の影と月の離角で、部分食、皆既食、あるいは月食は起きないかが決まります。地球の影の直径は約2度、角度の分で120分くらい、月の直径は約30分程度です。ですから、離角が60分よりも小さいと部分月食、さらに、30分よりも小さいところは、ほぼ皆既食になります。表内の「なし」部分は、離角が60分よりもほんの少し大きく、月食とならないのがわかります。
18年ごとの同じような時期に、同じ位の離角に地球の影と月が接近する---つまりは、同じような欠け具合の月食が起きる、というのは、なんだか面白い規則性です。この表は、それがわかるように表組みをしました。それで、中途半端に改列してしまっているわけですが、別の視点で見てみると、きれいにまとまっていると思いませんか?
サロス周期
この周期、古代バビロニアの時代から知られている、サロス周期と呼ばれるものです。
太陽と月は、6585.3日、18年と9~11日と8時間で、ほぼ同じ位置関係になることが知られています。日数があいまいなのに時間が8時間と決まっているのは、日数は18年間に何回うるう年が入るかで変わるためです。
この周期、日食や月食に関係なく、太陽と月は18年と10日前後で同じような位置関係になる、ということですが、特に、日食や月食があった日から18年と10日くらい経つと、また同じようなかけ方をする食がある、ということを教えてくれます。
| 日時 | 離角 | 種類 | 日時 | 離角 | 種類 | 日時 | 離角 | 種類 |
|---|---|---|---|---|---|---|---|---|
| 1992/12/10 08:43 | 0゚18′ | 皆既 | 2010/12/21 17:15 | 0゚19′ | 皆既 | 2029/01/01 1:50 | 0゚19′ | 皆既 |
| 見られない(地平線下) | 月食中に沈む(月没帯食) | 月食中に昇る(月出帯食) | ||||||
上の表は、サロス周期で列を変えて作ったものです2。ためしに2010年12月21日の月食に注目すると、1サロス周期前の月食は左隣の枠、1992年に起こり、1サロス周期後の月食は右隣の枠、2029年1月1日に起こることが分かります。また、元日に月食! 不吉!
図1の上側は、月食の時の、地球の影と月の関係を表しています。赤い大きな円が地球の影、その中に並ぶ小さな円が月。動きを表しています。3つを比べてみると、月はすべて、地球の影の上半分を通っていて、通り方もよく似ているのがわかります。
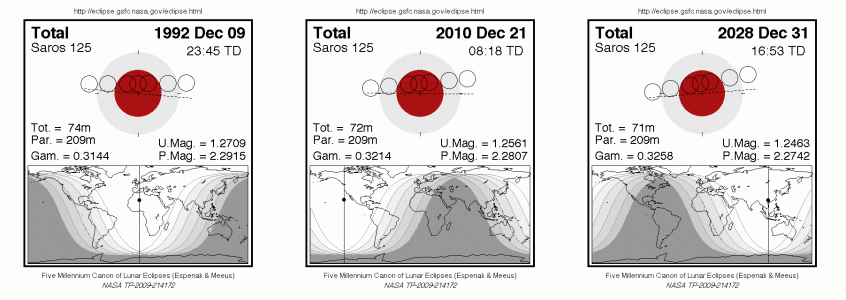
図1 1992年、2010年、2029年の月食の様子比較
NASA Eclipse Website
日食や月食を教えてくれるサロス周期には「.3」という端数がついています。これは日付の端数ですから、サロス周期が完全に1回りするには、1日の3分の1、つまり8時間程度余分な時間を必要とします。
今の3つの月食の時刻に注目すると、2010年には夕方に起こる月食が、1サロス周期前の1992年には明け方に、1サロス周期後の2029年には真夜中に起こることがわかります。
図1の下側、世界地図を見ると一目瞭然。灰色のところ、月食の見えない昼間の位置が、地球上を動いているのがわかります。
逆にいえば、8時間の端数を3倍すれば24時間。3サロス周期、54年と31日くらいで、同じ場所で同じ時刻に同じような食が見られるわけです。
図2は、2010年12月21日と、3サロス周期後、2065年1月22日の月食の様子。どちらも、夕方、東の空で起こる月食。かけ方も、地図の様子もよく似ています。
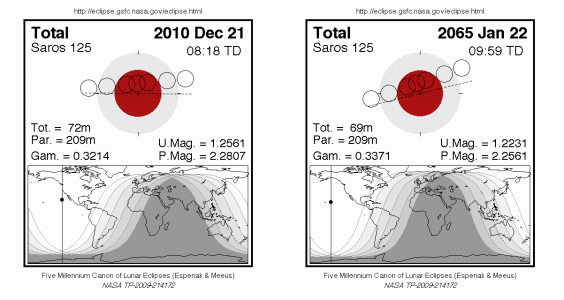
図2 2010年、2065年の月食の様子比較
NASA Eclipse Website
まったく同じにならないのは、端数がきっちり8時間ではないこと、3サロス周期後には季節も1ヶ月ほど進み、天球上での位置(なに座に見えるか)は変わること、さらに、地球と太陽が月を奪い合っているため3、月の軌道が微妙に変化することなどが理由です。
この、サロス周期を使うと、日食や月食が起こる日付がわかります。古代ギリシャのタレスは、日食が起こることを計算していたという記録もあり、2000年以上前から、日食月食の予報に使われていました。
これで、皆さんも日食や月食の予報ができるようになりました。周期が18年ですから、人の一生を考えると、ちょっと使いづらいところはありますが(子供が小学校に入学した年に起こった日食、同じように見られるのは54年後。子供が還暦を迎える(笑)というタイミング)、何かの役に立つ、かもしれません。
メトン周期
ところで、太陽と月関係の周期ではもうひとつ、メトン周期というのもあります。
月が、新月からまた新月になる時間は、ほぼ29.5日です。太陽が空の同じ場所に戻ってくるまでの時間は、ほぼ365日ですから、月の満ち欠けを単位とした1年は、365÷29.5=12と余り11で、12ヶ月と約11日と表されます。
毎年11日の余りを19倍すると、11×19=209、これを29.5で割ると、約7。毎年の余りも、19年経つとほとんど7ヶ月になります
つまり、12回、月の満ち欠けが起きた期間を1年として、19年の間に7回うるう月を入れれば、月の満ち欠けを月の単位とする、季節の変化とそう変わらない暦ができることになります。
紀元前433年にギリシャの天文学者メトンによって発見された、メトン周期です。
1年を12ヶ月とし、19年間に7回うるう月を入れる、というこのメトン周期は、いわゆる旧暦・・・太陰太陽暦にほかなりません。
今、私たちが使っている暦は、太陽暦、太陽の動きを基にした暦ですが、その今でも、毎日夜空を見上げて一番目につく変化は、やっぱり月の満ち欠けでしょう。
月の満ち欠けを基にした暦を使うというのはとても自然なことに思えます。実際、ほとんどの古代文明で使われています。
例外がエジプト文明ですが、ここは、ご存知のナイル川の氾濫の周期をおおいぬ座のシリウスを使って調べていましたから、もともとが太陽暦です。
農耕が始まったころから、暦の作成は非常に重要な仕事になったことでしょう。なにしろ、うまく季節に合わせて作物を作らなければ、飢えてしまいます。米が不作だからって、外米を緊急輸入するわけにもいきませんし4。むしろ、昔のほうが重要だったかもしれません。1日1日はっきりと変化のわかる月の満ち欠けで、1年を表すことができたら、とても便利で、しかも確実です。
古代の人々はきっと、一番分かりやすい目印である月の満ち欠けと、太陽高度などから求めていた1年とを、なんとしても結び付けたかったのだろうと思います。
今のように、望遠鏡もコンピュータもなく、観測を記録・保存することも難しい、数学の知識すら満足でない世界で、メトン周期やサロス周期を見つけ、今とほとんど変わらない暦を作ることができた、ということはとても素晴らしいことですね。
